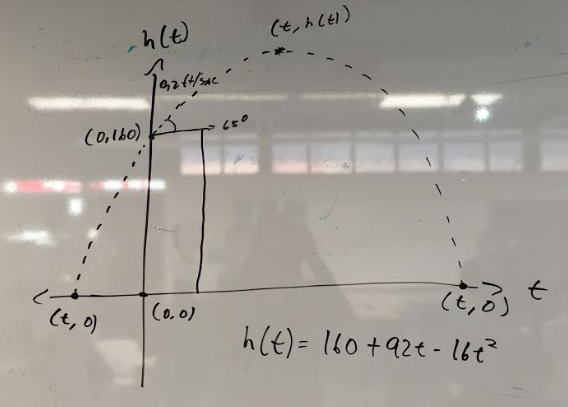
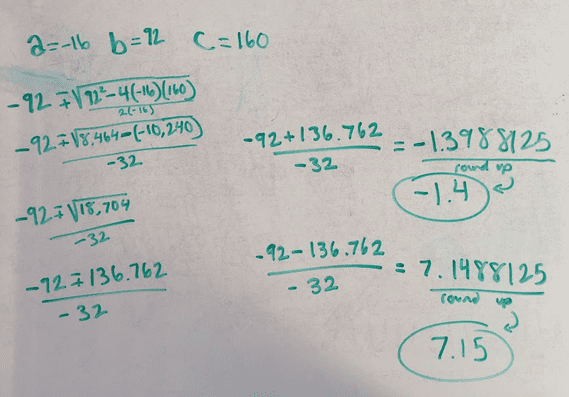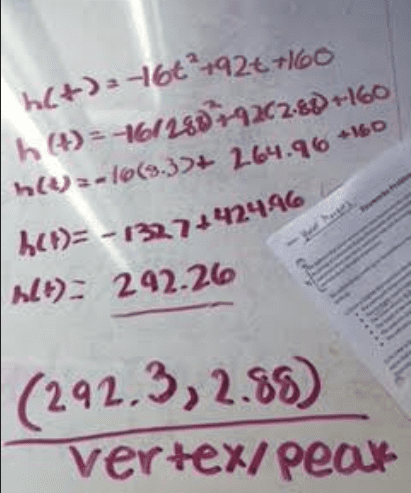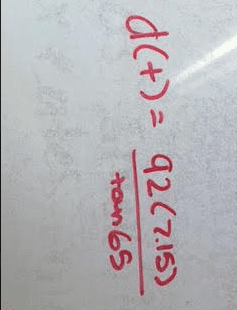A varsity soccer team had just won the championships and they wanted to celebrate this triumph by putting up a firework display. They're being launched from the top of the school tower and they need our help to make sure the spectators are safe and to calculate the timing mechanism that detonates the fireworks. To do this we must answer When will the fireworks reach theyre peak? And Where will the fireworks land? Also create a diagram representing the whole equation .We received a funtion representing the height of the fieworks and horizontal distance they travel. t in the equation represents time in seconds. Our function is h(t)=160+92t-16t^2
Problem and Solution
Before starting to solve the equation, we asked ourselves multiple questions such as what do the points in the story represent as points in an equation. For example, the unknown peak of the fireworks could be identified as the vertex or the unknown distance it will travel is associated with x-intercepts, lastly the height of the tower, where the fireworks were launched is the y-intercept.We took this information and built a graph on it, drawing what the problem gave us and ready to fill in the blanks. After all this is cleared, we could begin to solve the problem with more ease, knowing what parts represented what, and solving the equation with terms we've been familiar with all semester.
Here is the initial graph, next we have to fill in the blank spots !
First step to solving the equation was finding the x-intercepts! These are points on a graph that are on the x-line . There are many ways to find the x-intercepts but in this case we found that the quadratic formula might be the most convinient method. This formula allows us to find the roots of a quadratic equation , We plug in numbers from the equation to the formula, solve and bam! We have our x-intercepts (-1.4, 0) and (7.15,0).
Now what? |
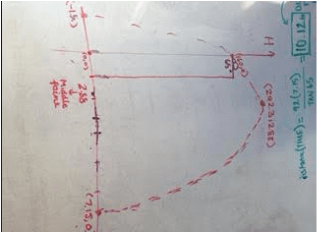
Whats next? Once the x-intercepts have been found the next step was to find the vertex. Parabola's are always symmetrical, so I knew the vertex would be in the middle of the x-intercept. To do this I took the two x-points and added them. Now I got 8.55 as the total distance between the intercepts, next we divided it by two to find the distance each point had to be from this middle point. This was 4.3, we then subtracted this by each point (1.4 and 7.15) and finally got the middle point 2.88 and placed that point on the graph.
|
We're so close... now we have x-intercepts and where the vertex is going to be on the x-intercept line. To find the height of the vertex, we have to plug the x-point (2.88) to the original equation and solve for height .
We've solved for the vertex we can now answer one of the initial question when will the fireworks reach their peak? (2.88, 292.3).
Where will the fireworks land?
We're all done with x-intercepts and the vertex of the fireworks, the last question to answer is where will the fireworks land? To solve for this we need to follow the equation d(t)=92t and plug then solve!
tan65
tan65
This part was easily done on the calculator, multiplying 92 x7.14 (7.14 represents the time on the graph) then divide it by the tan of 65. You can find a tan button on the calculator. We can now answer the last question when will the fireworks land? They will land 306.69 feet in 7.14 seconds.
Overall this problem was really fun to solve, it pushed my thinking in a way where I had to relate this real life scenario to a math equation. Something I got out of this problem was learning how and when to use the quadratic formula, and memorizing the formula.
If I could grade myself on this quadratics unit I believe I should receive an A. This is because ive worked really hard on understanding the material,always asked questions when I was in doubt and helped others who needed it.