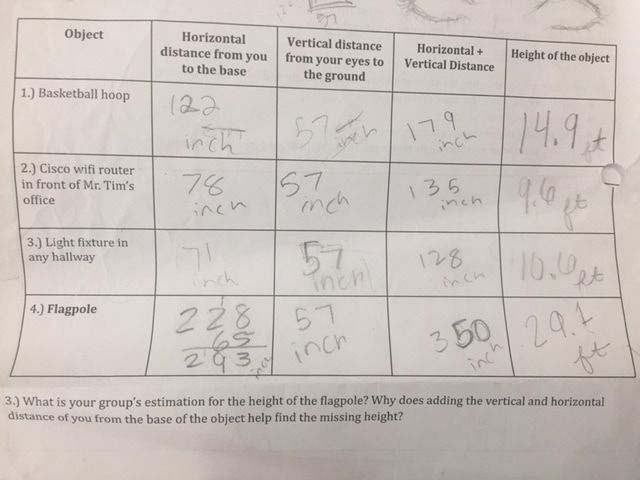
Problem Statement
The schools wants to get a new flagpole and realize there is a lot of calculations that have to be made before installing a new one. In order to correctly replace our flagpole, we need to take some measurements like the height of the flagpole. Asking around, nobody actually knew the length of the flagpole standing right outside our school. Our team decided we would discover the mysterious height of High Tech High's flagpole using 3 different methods.
Initial Guess?
So before making any calculations at all, we came up with our own estimations of what we thought the height was just by looking at the pole. My guess was around 40 ft. My thought process was to see how many times I can stack my 5 ft friend on the flagpole using squinting and my fingers. Now going back into the class room the first thing we learned before getting to our 3 method's was....similarity. Similarity between polygons basically means two shapes are exactly the same, but smaller of bigger. In order to be similar they need to have proportional sides and the same angles.
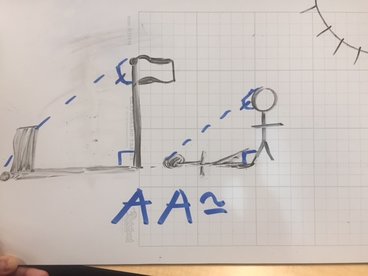
This was the first method we learned. In the Picture above you can see the flagpole and its shadow and also a person and it's shadow. Our idea was to find a triangle in this diagram , prove similarity and then create a proportion to solve for the missing height. We were able to prove similarity using a similarity theorem known as AA~ (angle, angle), which is only relevant with triangles. It basically states that if two triangles share 2 same angles, they are automatically similar . The angles I was able to spot were the right angle connected by the object and base of shadow, and the sun is pointing down in the same directions towards both objects, therefore they create the same angle. We calculated our partner Sam's shadow and height, then the flagpoles shadow and created a proportion to solve for x, flagpoles height. Here are our results...(22 ft)

sorry the picture is a little messy but here I basically just found heights of objects such as a mini pole, my peer and set proportions with their height, their shadow , to the shadow of the flagpole and having x be the height of the flagpole.
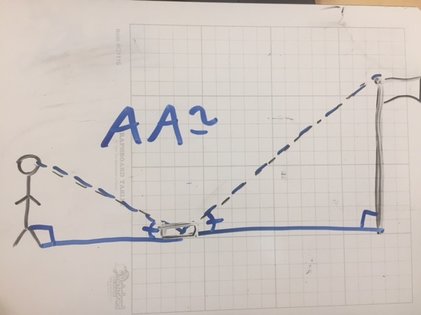
Our second method states that you can use a mirror and the principle of light reflection to measure the heights of objects, all that is needed it a flat surface to place the mirror. After laying the mirror on the group some distance from the object you're trying to measure, you move slowly away from the object, looking at the mirror until you can see the object in the mirror. Now that you're in this position you can create two similar triangles because of AA~ again, there is the right angle between the base of the objects and the ground, then the angle of the reflection through the mirror is the same .
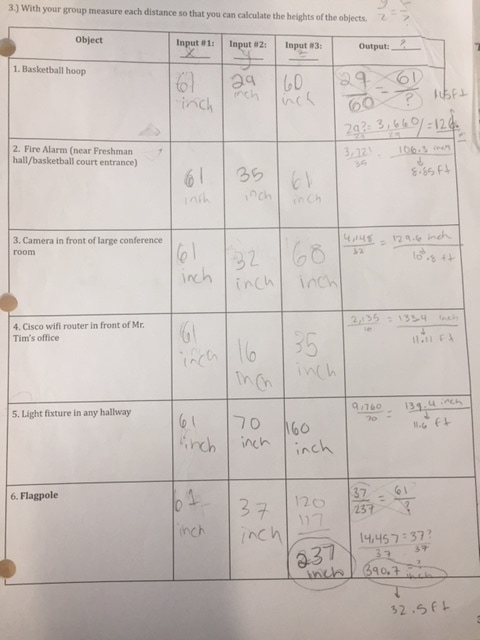
Now here are our calculations of objects throughout the school using this method, and the flagpole. (32.5 ft)

This next method is based of the properties of an Isosceles triangle and the fact that is has two congruent base angles. And we looked more specifically at right angled isosceles triangles, where we knew the other two angles were 45 degrees for sure. So we used our teaches DIY clinometer, which is a tool that is used to measure really tall things like buildings and things you cant measure because are too tall. So we had one of our partners look into the straw and spot the top of the flagpole or object, then I read the angle measure on the clinometer until it reached 45 degrees, as she moved back and forth. Now we take measurements such as the distance between you and the object, and the ground to your eyes because the most accurate triangles finish at your feet not your eyes. Now adding both of these measurements and converting it to ft had us at the height of the flag pole. (29.1 ft)
So my final guess of the mysterious height of the flagpole would have to be 22 feet, which is supported by the shadow method. This method overall seems the most accurate to be because it has less room for error. For the mirror method , there wasn't an exact measurement, when looking down in the mirror to spot the object it was always "oh, around here" and you had room to move around and still see the object. This gives the impression that its only a rough estimation. Next, the Clinometer method seemed really reliable to me, especially considering that's what people use to measure buildings, however ours was a DIY (do it yourself). The string that told us the angle seemed unreliable and was thick, so it was covering a few angle measurements, so it was hard to tell when it was exactly at 45 degrees. With all this in mind, I figured the shadow method was most reliable. It just made sense to me and is what I would use in the future to measure something I cant reach.
Problem Evaluation
I really enjoyed this problem, I would say confidently it was my favorite math problem of this school year. It pushed my thinking in a way I hadn't had to before, I had to look at the world and scenarios in triangles. It was super cool and crazy to me that we can take something we're learning in class and apply directly outside, where we were measuring and learning in such a hands on way. I also really had to think about why it worked and how, that required a lot of focus and concentration. A lot times in math class or any class i'm sure people ask themselves "why do I need to know this, I'm never going to use this in real life", because I have plenty of times. But that didn't cross my mind at all, in fact it was the opposite, I think now i'm going to walk around knowing I can measure that tall building in minutes, or the tree in front of my house.
Self Evaluation
So I believe I deserve an A this unit. I really found myself contributing to my group, helping make sure everybody understood what was going on and why it worked. At times I saw my classmates confused of they would ask "wait, why does that work?" And I always made sure they got it. I also believe I deserve this grade because I really tried hard throughout the unit. While we went out to take measurements I was on task, during class I used the time productively and overall put my mind into the lessons to makes sure I understood everything.
Edits
Now before publishing this weebly I received a few peer critiques and this is what they suggested...
-Space out pictures
-Misspelled words
-Explain in more detail my initial guess
-Space out pictures
-Misspelled words
-Explain in more detail my initial guess