Problem Statement
The task is to find a general rule or pattern to determine which chair a knight should try to sit in to become the winner at King Arthur’s table.
The way King Arthur chooses the winning knight is by sitting them at a round table and going around the table telling the first knight he is in and the next knight he is out and so on. The knights that are out are removed from the round table, and the rest stay in until King Arthur says, “You’re out.” Depending on what he says to the previous knight, the next knight is either in or out; therefore, if he says, “You’re out” to one knight, King Arthur will say, “You’re in” to the next knight around the table. King Arthur continues the game in this fashion, regardless of how many knights are at the table, until only one knight is left at the round table. The last knight remaining at the round table is the winner of the evening.
There is a different winning “seat” depending on the number of knights there are, and in order to figure out which chair a knight should sit in to become the winner, one must find a pattern or formula. The task is to find this pattern.
The way King Arthur chooses the winning knight is by sitting them at a round table and going around the table telling the first knight he is in and the next knight he is out and so on. The knights that are out are removed from the round table, and the rest stay in until King Arthur says, “You’re out.” Depending on what he says to the previous knight, the next knight is either in or out; therefore, if he says, “You’re out” to one knight, King Arthur will say, “You’re in” to the next knight around the table. King Arthur continues the game in this fashion, regardless of how many knights are at the table, until only one knight is left at the round table. The last knight remaining at the round table is the winner of the evening.
There is a different winning “seat” depending on the number of knights there are, and in order to figure out which chair a knight should sit in to become the winner, one must find a pattern or formula. The task is to find this pattern.
Process
First approaching this solution by myself, I drew King Arthur's table, labeled 10 seats and played the In/out game. From this, I discovered the first rule, always sit on an odd number seat. The first round of IN/out removes all even number, which mean they have 0% chance of getting picked. I also discovered for 10 players the winning seat was 5.
Next, when I approached this with a group we began making an organized table with two variables. x represented the number of knights that sat around the table , and y represented the winning seat number. We did this up until 32 players. We saw a pattern with the winning seat. It was increased,( not that consistently) and then reset, back to 1, repeating this pattern. We also decided to take note of the difference between x and y, something that was also consistent. It followed the same pattern of increasing, and then resetting.
During a class discussion we discovered the winning seat would reset"at every number with the base of 2. ( 2,4,8,16,32). So every time x was a base of 2, the winning seat was one. The number of the winning seat then increased by 2, steadily until the next "reset". As the winning seat increased by 2, the difference between x and y steadily decreased by 1 each time until it hit 0, which was the number BEFORE the reset. And determining how close x was to the base of 2, determined the y, the winning seat, something that had to do with the solution.
Next, when I approached this with a group we began making an organized table with two variables. x represented the number of knights that sat around the table , and y represented the winning seat number. We did this up until 32 players. We saw a pattern with the winning seat. It was increased,( not that consistently) and then reset, back to 1, repeating this pattern. We also decided to take note of the difference between x and y, something that was also consistent. It followed the same pattern of increasing, and then resetting.
During a class discussion we discovered the winning seat would reset"at every number with the base of 2. ( 2,4,8,16,32). So every time x was a base of 2, the winning seat was one. The number of the winning seat then increased by 2, steadily until the next "reset". As the winning seat increased by 2, the difference between x and y steadily decreased by 1 each time until it hit 0, which was the number BEFORE the reset. And determining how close x was to the base of 2, determined the y, the winning seat, something that had to do with the solution.
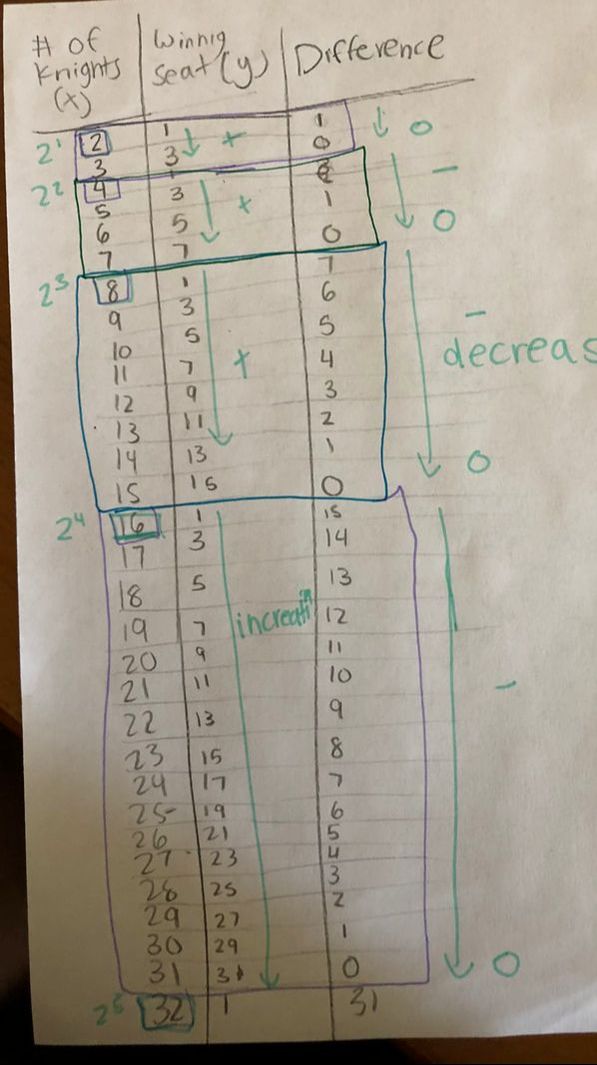
Here is the table we were able to come up with. I noted the different patterns that we found.
Solution
Even after finding various patterns in the math problem, finding an equation was very challenging. We knew every time the number of knights was a base of two, the winning seat was 1, resetting the pattern of increasing by 2. We also noticed the pattern, when looking at the difference of x and y, it would consistently decrease by 1 until hitting 0, before the reset button.. We also knew to never sit on a even number, the equation we come up with, y can never be an even number.
We ended up not finding an equation for this math problem, however we did notice a lot of patterns that we were able to make accurate guesses on what the winning seat would be.
We ended up not finding an equation for this math problem, however we did notice a lot of patterns that we were able to make accurate guesses on what the winning seat would be.
Reflection
The most challanging part of King Arthur's math problem was finding the equation. We did not even find an equation at all, showing how difficult it was for me and my group. It was especially frustrating because it seemed to simple, and we KNEW there were patterns but it was just and unknown territory so we did not even have an idea of what the equation should look like. It was very frustrating, and I can't help but to feel like we failed by not being able to come up with a equation.
Working with my group, I think we worked well together. We were willing to support each others idea, share and listen. I think because of this, I was more motivated to find a solution with them.
I think I deserve an A as a grade because I contributed to making my groups environment inviting by asking questions to each other and supporting ideas everyone came up with. I also came to math prepared to learn and challenge my thinking.
Working with my group, I think we worked well together. We were willing to support each others idea, share and listen. I think because of this, I was more motivated to find a solution with them.
I think I deserve an A as a grade because I contributed to making my groups environment inviting by asking questions to each other and supporting ideas everyone came up with. I also came to math prepared to learn and challenge my thinking.
